3B1B: Essence of Linear Algebra
1: Vectors
3 main ideas surrounding vectors.
- vectors - arrows pointing in space - has length and directon position does not matter can be 2D and 3D.
- vectors - ordered list of numbers - i.e vector fancy word for list
last one i dont resonate with but here it is regardless. i dont really get it ig.
- vectors - can be anything as long as there is an addition and a multiplication operation possible.(Multiplication by a number). ok this is abstracting away from the representation. that is its purpose.
think of vectors as the 1st idea in a coordinate system with its tail(the part without the arrow) rooted at the origin
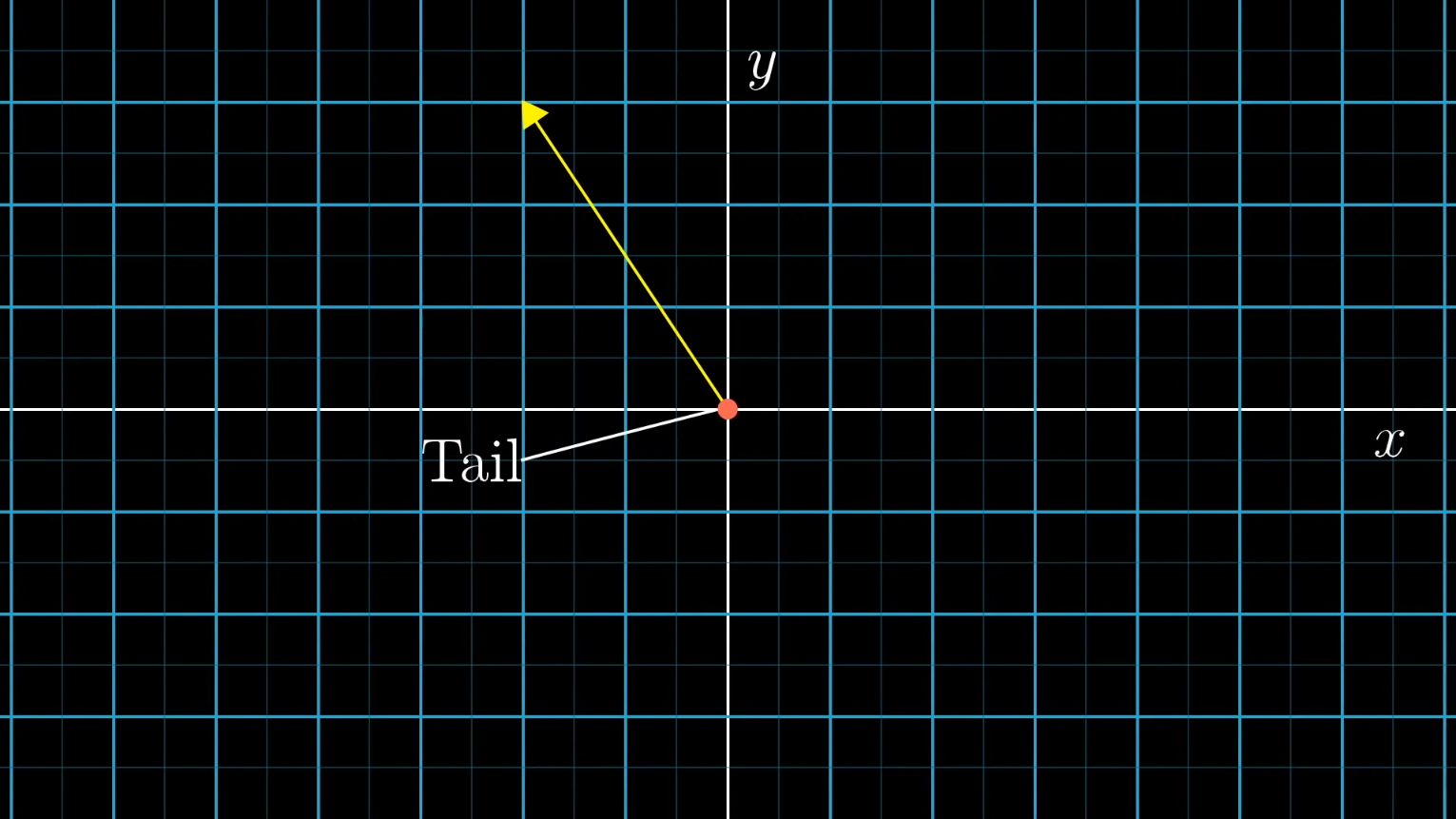
the goal is to understand concepts using this coordinate plane idea and then transfer that to the list of numbers idea.
know this idea already. how to represent vectors in a cordinate plane.
[coordinateAxe1 coordinateAxe2 coordinateAxe3 coordinateAxe4 …] -> Number of coordinate Axes -> Dimensions
[x y] -> 2D
[x y z] -> 3D
this addition of vectors visualization is cool.
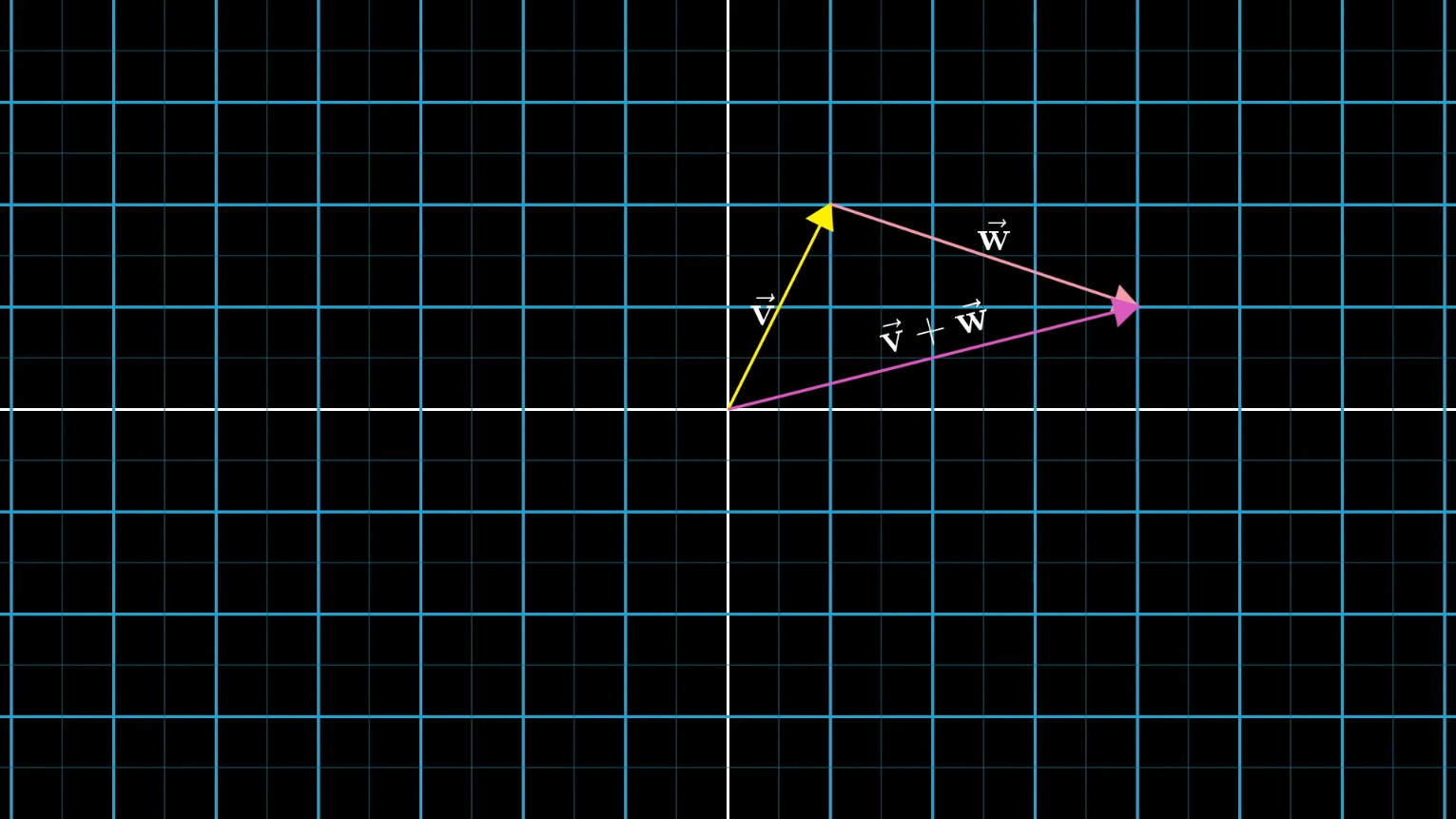
COOL IDEA ALERT!!
think of vectors as movement in space with a direction and a magnitude.
same idea can be applied to the number line obv
[x1 y1] + [x2 y2] = [x1+x2 y1+y2]
multiplication of a vector by a number is streching the vector if the number is >1, shrinking the vector if the number is <1 and the same for negative numbers but the vector is flipped first.
this operation can be called scaling (for obvious reasons) and the number which scales the vector is called a scaler!
throughout linear algebra one of the most common things numbers do is scale vectors. so scaler <-> number
2[x y] -> [2x 2y]